基于最大风险承受能力的期货投资组合
发表于2015-04-15 10:11:03
模型一：基于最大风险承受能力的期望-VaR组合模型
模型二：基于最大风险承受能力的期望-CVaR组合模型（改进）
适用投资标的：股票、股指期货、国债期货、商品期货
适应投资对象：需要股票和期货市场进行均衡配置的投资者
摘要
在以往的投资决策和资产选择研究中，虽然多数研究都假设投资者具有风险规避的特征，但却忽视了“死亡风险”的存在以及投资者对“死亡风险”的重视。这种状况不仅明显存在逻辑上的非一致性，而且也与实践脱节。宏观上来说，随着金融创新的不断推进，投资“杠杆化”趋势的不断增强，以及由“杠杆化”引发的更为紧密的经济联系，使投资者“死亡风险”可能成为引发金融危机的重要来源。微观上来说，在期货及衍生品市场，发生爆仓的投资者非常常见。因此，无论在理论上还是在实践中，对“死亡风险”的研究变得愈来愈迫切。
本文试图通过将“死亡风险”问题对应转化成行为人或者投资者的最大风险承受能力问题，结合VaR最新理论进展，从行为金融学的视角来研究投资者的资产选择及其风险控制。即建立基于最大风险承受能力约束的期望—VaR组合模型和基于最大风险承受能力约束的期望—CVaR组合模型，并通过该模型寻找最优投资组合。主要内容包括：
一、“死亡风险”、最大风险承受能力、VaR的经济联系及其核心内容的一致性；
二、基于行为金融学视角的最大风险承受能力约束下的投资组合模型构建及求解；
三、实证分析。
无论从理论分析还是从经验证据上看，基于最大风险承受能力约束的期望—VaR组合模型和基于最大风险承受能力约束的期望—CVaR组合模型都是对传统投资组合模型的进一步修正，且基于最大风险承受能力约束的期望—CVaR组合模型要相对优于基于最大风险承受能力约束的期望—VaR组合模型。
关键字：死亡风险；风险承受能力；期望—VaR ；期望—CVaR
一、研究背景及意义
从大的视角看，近几十年来世界范围内金融危机频发，如1987年美国股市的“黑色星期一”，1995年的巴林银行破产，1997年的亚洲金融风暴，2007-2009年由美国次贷危机导致的全球金融危机，2010年的欧债危机等，这些危机所具有的共同特征是影响大、范围广、时间长且事件发生之前，很难对其进行准确的预测。过去，我们一直认为，此类事件发生概率极小，通常被称之为极端事件。但事实是，过去被我们称之为小概率事件的东西却在今天似乎变得越来越常见，一些被认为不朽的金融参天大树一夜之间倒塌。从微观视角来看，对于很多致力于期货及金融衍生品市场的投资者来说，爆仓事件屡见不鲜。
无论从极端事件发生频率的变动趋势，还是从这类事件的影响后果分析，无论是金融监管层，还是我们个人投资者，都应该对这类事件的风险即“尾部风险”给予足够的重视。
很多时候“死亡风险”都是以“尾部风险”的形式出现，即泛指那些不太可能发生，但一旦发生则代价相当高的风险，很多投资者在突发的小概率事件期间导致各类资产价格大幅暴跌，遭受重大经济损失时，才意识到“尾部风险”的影响之大。在每一次重大的金融危机的背后，其实都是无数个投资者盲目参与，没有从自身风险承受能力出发，不重视“死亡风险”，非理性的做出了超过其自身最大风险承受能力的投资决策而导致的。
随着“死亡风险”爆发的频率越来越高，作为投资者或资产管理者，我们在做投资决策时，就很有必要把我们自身最大风险承受能力和“死亡风险”可能带来的影响作为重要决策依据之一认真考虑。
在以往的投资决策和资产选择研究中，虽然多数研究都假设投资者具有风险规避的特征，但在风险控制的讨论中，往往只注重了正常情况的资产价格波动或风险，忽视了“死亡风险”的存在以及投资者对“死亡风险”的重视。这种状况不仅明显存在逻辑上的非一致性，而且也与实践脱节。因此，无论在理论上还是在实践中，将“死亡风险”因素纳入资产组合选择的研究，不仅对于完善资产选择理论具有重要的意义，而且对于指导投资者的风险控制实践具有重大的现实价值。本文试图在这一方面做一些偿试，以期从理论上给予“留得青山在，不怕没柴烧”的中国谚语一个合理的证据。
二、“尾部风险”、“死亡风险”与最大风险承受能力
传统的金融风险管理研究往往只注重正常状态下的风险管理问题，而忽略了投资者对极端事件风险的重视，马科维茨的均值-方差范式从平均的角度来量度风险，均值度量虽具有全面性综合考量的优点，但一个明显的缺陷是它会隐盖极端事件发生给投资者可能带来的灾难性后果。现代行为金融学的研究给予了这种极端事件应有的重视，所谓“尾部风险”的研究就是一个很好的证例。然而，“尾部风险”注重的是风险的度量，它忽略了投资者承担风险能力的差异，不同风险承受能力的投资者，其对待“尾部风险”的态度显然是不同的，即当投资者面对“生与死”的考虑时，才会对“尾部风险”给予特别的关注。
在保险精算和医学领域，通常把因重大突发事件或疾病导致自然人失去生命的风险称作死亡风险。如果将人的自然生命延伸为“经济生命”，则我们就不难将死亡风险概念引入到金融领域的研究中。即将因重大突发事件的发生而导致行为人或投资者投资活动“死亡”的风险称作金融投资活动中的“死亡风险”。或者说，对于那种超过行为人最大风险承受能力，使其之前的投资活动难以再继续的风险称为“死亡风险”。很多时候“死亡风险”都是以“尾部风险”的形式出现，即泛指那些不太可能发生，但一旦发生则代价相当高的风险。
随着“死亡风险”爆发的频率越来越高，作为理性的投资者或资产管理者，在做投资决策时，就很有必要把自身最大风险承受能力和“死亡风险”对应起来考虑，将投资方案选定在，即便是出现最坏状态，其损失也能被控制在最大风险承受能力的范围内。
近年来，我们有时候可以在新闻上或互联网上看到关于投资者在金融市场上投资或投机失败自杀或者犯罪的报道。其实，那些人的绝对损失在那场投资活动中并不一定是最大的，相比巴菲特或李嘉诚在某次股市大跌时的资产价值缩小相比，只是九牛一毛，但为什么为导致他们失控做出不理智的举动？原因很简单，损失超越了他们自身风险承受能力。那么，仅仅用绝对损失来衡量投资者风险承受能力是很不准确的。为此我们用相对损失来定义行为人的最大风险承受能力，具体如下：
设投资者或行为人的初始财富为W，其能够承受的最大损失为L，则定义该行为人的最大风险承受能力为：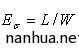
其中，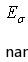
为风险承受能力，其实就是最大损失占其财富的比重。
三、VaR计算与风险管理
VaR（Value at Risk）通常被翻译为风险价值或在险价值，通俗的来说， VaR值是指：在给定的显著性水平p下，在持有期限t日内，预期最大潜在损失。在20世纪90年代，VaR极受银行业和其他一些金融机构关注，该风险管理技术主要借助统计学的思想和方法来评估金融机构所持有的金融资产价值中暴露于风险中的风险大小，可以为金融机构实施有效的风险管理提供决策依据。
VaR本质上就是在常态风险下，也就是金融机构或投资者面临“正常”的市场波动时，基于一定置信水平的资产组合可能遭受的最大损失值。通过VaR，我们可以直观的知道我们的资产所面临的风险具体有多大，结合我们自身投资需求和风险承受能力，我们可以根据VaR进行投资决策选择和优化资产配置，从而实现有效的风险管理。
使用VaR进行风险管理，其关键取决在于VaR的计算，目前计算VaR的方法主要有两大类：一类是使用参数法计算VaR；另一类是使用模拟法计算VaR。参数法，此方法假定资产收益率分布服从正态（其“参数”性质主要来源于该方法依赖于特定分布假定这一事实）。常见的四种不同的参数方法分别为：组合—正态法、资产—正态法（RiskMetrics模型采用的方法）、δ—正态法和δ—у法。模拟法计算模型主要可以有两类：历史模拟模型和蒙特卡罗模型。由于目前探讨VaR算法的参考资料很多，本文不作具体讨论。
在风险管理中，投资者最大风险承受能力越大，即可以接受更大的VaR值，这个时候，只要我们使我们计算出的VaR值不超过行为人的最大风险承受能力，即可以做到有效的风险管理。而当发生极端事件时（小概率大损失的事件），也就是发生我们前面讨论的“尾部风险”时，此时的损失值通常会大于上面计算出的VaR值，这个时候如果没有采取足够的风险管理措施，通常会导致“死亡风险”的发生，此时损失通常会超出行为人的最大风险承受能力。为管理死亡风险，后面引入CVaR继续进行模型构建和分析。
四、基于最大风险承受能力约束的期望—VaR组合模型
4.1 模型构建
设投资组合收益率向量为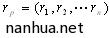
且服从从多元正态分布,投资组合的资产权重向量为
。∑为rp的方差—协方差矩阵,A为投资组合中各资产收益间的相关系数矩阵。则在置信水平为p的条件下,有投资组合P的VaR为：
4.2 期望-VaR模型求解
在上述模型中，如不考虑最大风险承受能力约束时，可以简化如下：
显然，（4.2.3）式是一个含有n+2个未知量的线性方程组，为了方便分析讨论，这里将（4.2.3）式写成矩阵的形式。并令
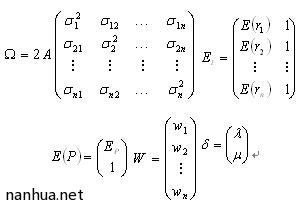
4.3 基于最大风险承受能力约束的的期望—VaR组合模型的求解
由前面的内容讨论可以知道，我们在组合模型中，只是简单的从理论的角度推导有效边界，进而找到最优解，并不一定能够满足投资者本身的需要。从行为金融学的角度来说，投资者风险偏好不同，对资金的流动性需求不同，当然对风险的承受能力也是千差万别。带有最大风险承受能力约束的模型为4.2.1式。其实，该模型只需要将前面期望—VaR模型的最优解，分别和最大风险承受能力的值作比较，就很容易发现解是否符合投资者的需求或找到符合投资者需求的最优解。
五、基于最大风险承受能力约束的期望-CVaR组合模型
尽管期望—VaR模型所推导出的有效边界和马克维兹的的有效边界是一致的，最优解也具有很好的特征和性质，且纳入最大风险承受能力约束以后，可以从行为金融学的角度找到符合投资者实际需要和风险偏好的资产组合。但是我们知道，使用VaR度量投资组合收益率的风险，虽然克服了马克维茨的传统的均值—方差范式分析方法的缺陷，可是VaR本身的缺陷却无法克服，即风险值 VaR 只反映一项资产或资产组合在一定的持有期内给定的显著性水平下潜在的最大损失，而对于一些处于极端情况下的潜在损失，用 VaR 无法度量，也就是我们前面探讨的引发“死亡风险”的小概率事件。虽然这种“死亡风险”发生的概率非常小， 但一旦发生，有可能超出投资者的风险承受能力，将给投资者带来灭顶之灾。针对 VaR 方法的缺点的改进， Rockafellar 等提出了一种新的风险度量方法，即条件风险价值( CVaR)方法。所以我们接下来试着从控制“死亡风险”的角度出发，，将 CVaR 方法及最大风险承受能力引入期望-CVaR范式中， 结合我国实际情况，做一些合理的假设，以投资组合收益率的CVaR 最小为目标函数， 以最大风险承受能力为约束条件，构建基于最大风险承受能力约束的期望
组合模型，并对模型的求解进行探讨。
5.1 条件风险价值（CVaR）主要思想及性质
5.1.1条件风险价值（CVaR）含义
CVaR是 Conditional Value at Risk 的缩写， 一般翻译为条件风险价值，也可称之为平均超额损失( Mean ExcessLoss) 或尾部 VaR(Tail VaR) ，其含义可理解为: 在一定的显著性水平下(置信度) ， 损失超过VaR 的潜在值．下面用形式化的语言来描述其含义。
设x为资产组合中各资产所占的比重（即权重或头寸），向量y为影响损失的市场因子，比如收益率，其中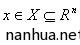
，X为可行集，且决策向量x下的损失函数为f(x,y)。则对任意一个x，由 y 导致的损失f(x,y) 是在R上服从某一分布的随机变量。
为讨论方便，先设 y对应的概率密度函数为p(y) ，则潜在损失f(x,y) 不超过某一特定阈值β的概率可以表述为:
5.2 构建基于最大风险承受能力的期望-CVaR组合模型
以控制“死亡风险”事件的发生为出发点，尝试构建基于投资者最大风险承受能力约束的投资组合模型。首先，我们做以下假定：
假设1：投资者在投资过程中选取了n 种资产进行投资，其中1 种为无风险资产且投资比例大于0，其余n-1种为风险资产，且风险资产的收益率服从正态分布。
假设2：为了更好的分散风险，假定投资在第i种风险资产上的资金占资产总额的比例上限为m，其中0<m<1。
5.3模型的求解
对于上述期望-CVaR模型，我们分以下2 个步骤对其进行求解。1）先对有投资比例限制约束的均值-CVaR 模型进行求解，并试图找到基于其约束的资产组合有效边界。2）然后纳入约束条件最大风险承受能力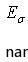
，进一步进行求解。
由于该模型的理论求解过程过于偏学术且篇幅较大，本文主要讨论该模型的实用性，而且后面实证部分通过MATLAB软件进行求解，所以这里不对理论求解过程作详细讨论，如有需要，可与本人联系。
六、实证分析
6.1 相关假定和变量说明
为更好的探讨基于最大风险承受能力约束的期望—CVaR—E模型特点，做如下假定：
假定1：不考虑投资比例限制；
假定2：不考虑无风险资产；(此假定并不影响我们对期望—CVaR—E模型实质性的讨论)。
假定3：交易方向只做多；
假定4：不考虑通货膨胀；
假定5：最大风险承受能力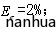
假定6：不考虑交易成本。
则可以把基于最大风险承受能力约束的 期望-CVaR-E模型简化如下:
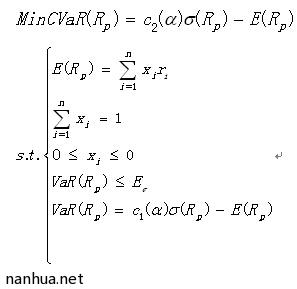
6.2 样本选取及数据预处理
为了分散风险，使得所选样本具有代表性，我们选择期货市场中品种相关性较小且流动性较大的品种：（数据取自通达信）
（1）沪深300股指期货（取IF加权,代码IF）
（2）5年期国债期货（取TF加权，代码TF）
（3）锌期货（锌指数，代码ZN）
（4）天然橡胶期货（橡胶指数,代码RU）
（5）螺纹钢期货（螺纹钢指数,代码RB）
（6）豆粕期货（豆粕指数,代码M）
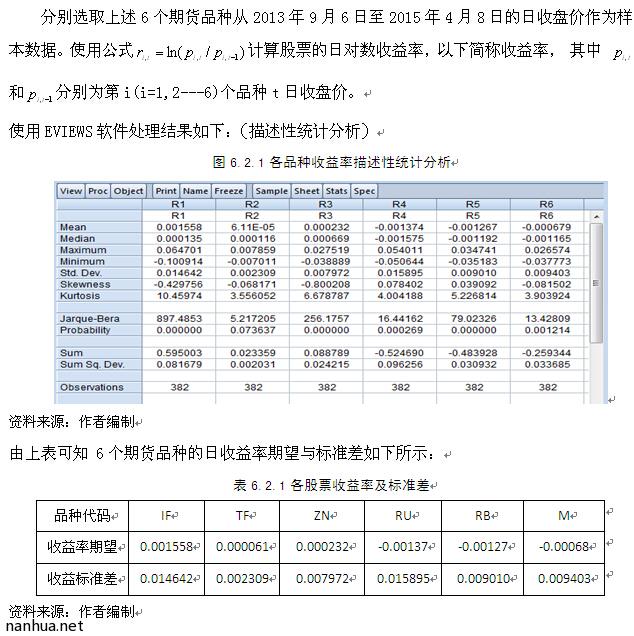
6个期货品种收益率协方差矩阵为:
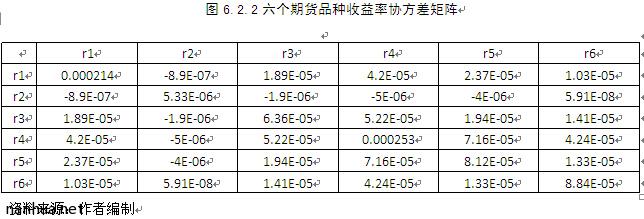
6.3 模型求解与分析
则可以通过MATLAB分别求得其对应最优解如下：
首先，从模型求解的结果来看，当组合期望收益超过0.0020时，该模型没有合适的解，当然，这是显而易见的，因为6个期货品种当中，期望收益最高的，即股指期货，仅有0.001558，所以当组合期货收益要超过这个，显然是无法实现的。
具体来看，由上表可以看出，随着组合期望收益率的提高，在第一个品种，即股指期货上配置的资金比例不断增加，在收益率为0.0005时，配置在股指期货上的资金比例为0.2828，而在收益率为0.0030时，配置在股指期货的资金比例达到了0.9567，当然主要原因是，在6个期货品种中，股指期货的期望收益是最高的。第二个品种，即国债期货，其期望收益不高，但是波动率很低，所以在国债期货上的配比是随着组合期望收益提高而降低。在组合期望收益在0.0005时，在国债期货上的配比为0.6229，而在期望收益升至0.0030时，在国债期货上的配比下降至0.001565。其他4个品种也呈现期望收益、风险与资金比例类似的逻辑关系。
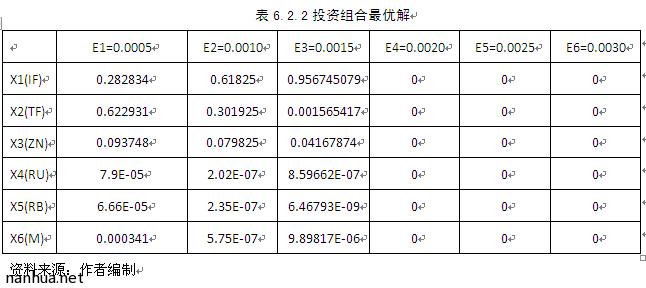
（2）基于最大风险承受能力的投资组合选择
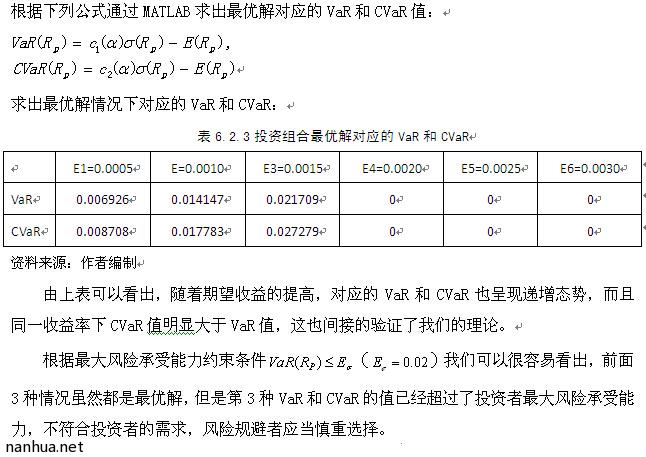
七、结论与展望
本文从 “死亡风险”的含义及风险特征出发，通过对“死亡风险”与最大风险承受能力的比较分析，将“死亡风险”转化为最大风险承受能力。在此基础上，详细讨论了最大风险承受能力与VaR的关系，借助VaR的传统算法和最新进展，从行为金融学的视角来探讨基于最大风险承受能力约束的期望—VaR组合模型和基于最大风险承受能力约束的期望—CVaR组合模型，并详细讨论了两类模型的理论求解及实证分析。
在探讨上述模型的构建、求解、实证等分析过程中，我们发现，在收益确定的条件下，上述两种模型的资产组合最优解得有效前沿和马克维茨均值方差模型的有效前沿形状类似，这说明这三种范式讨论的结果是一致的。而且在收益率一定时，明显有CVaR值大于标准差VaR值，VaR值大于方差。
从数理的角度看，期望—CVaR范式与期望—VaR范式、期望—方差范式相比，收益率上限低于其他两种方法，而下限大于另两种方法，这表明 CVaR作为约束条件使投资组合的有效边界减小了，从而证明了在 CVaR条件下比另外两种条件下更能体现投资组合的潜在损失，说明 CVaR作为目标条件比其他2种方法更为保守和安全， 更接近投资者的心理习惯，因此CVaR比其他模型更符合实际。
在期望—CVaR范式下，把最大风险承受能力作为约束条件，寻找到的最优资产组合不仅是有效边界上的解，而且是符合投资者需要的，即可以把潜在最大损失控制在投资者最大风险能力可承受范围之内。
无论从理论分析还是从经验证据上看，基于最大风险承受能力约束的期望—VaR组合模型和基于最大风险承受能力约束的期望—CVaR组合模型都是对传统投资组合模型的进一步修正，且基于最大风险承受能力约束的期望—CVaR组合模型要相对优于基于最大风险承受能力约束的期望—VaR组合模型。
为了研究问题的方便，在构建和求解模型过程中，我们依然假定各资产及资产组合服从正态分布，而事实上，很多研究都已经通过实证表明，大部分时候资产收益率具有明显的高峰后尾特征，并不服从正态分布，所以该模型所得的结论与实际相比，可能会有一定的误差，严重时甚至会产生系统性偏差，这不仅是本文的不足，而且也是我们以后要进一步研究和改进的方向。
参考文献
[1] 李腊生.不确定性决策与金融资产投资[M].广东人民出版社，2002。
[2] 李腊生，翟淑萍.现代金融投资统计分析[M]第二版.中国经济出版社，2009。
[3]李子奈.计量经济学[M]第二版.高等教育出版社,2000。
[4]胡支军.证券组合投资决策模型研究[M].西安交通大学硕士学位论文，2005年12月。
[5]高铁梅.计量经济分析方法与建模[M].清华大学出版社，2009年5月。
[6] 简.菲利普.鲍查德，马克.波特.金融风险理论[M].经济出版社，2002年8月：28-35.
[7] 威廉.F.夏普.投资学 [M]第五版.中国人民大学出版社，1998。
[8] 小詹姆斯L.法雷尔.投资组合管理理论及应用 [M] 第二版.机械工业出版社，2000。
[9] 皮埃特罗•潘泽，维普.K.班塞尔.用VaR度量市场风险[M].机械工业出版社，2001。
[10]李腊生.概率分布设定风险与投资选择[J].上海立信会计学院学报（双月刊），2009年第4期。
[11]李腊生.不确定性的经济学思考[J].经济科学，2002年第1期。
[12]周孝华，唐秋燕.沪深300指数极值VaR的分析与计算[J].统计观察，2008年第10期。
[13]王晶，张裕生.均值—CVaR优化模型在投资组合中的应用[J].枣庄学院学报，2010第27卷第二期。
[14]王波，高岳林.基于CVaR度量的投资组合优化研究[J].武汉理工大学学报，2012年2月第34卷第一期。
[15]钟纯，吴雪.基于VaR和VaR下优化模型及其在保险资金组合投资中的应用[J].南昌大学学报，2011年第33卷第4期。
[16]左志鹏基于CVaR约束的投资组合模型及应用分析[J].长沙大学学报,2011年第25卷第二期。